Recent contextual word embeddings (e.g. ELMo) have shown to be much better than “static” embeddings (where there’s a one-to-one mapping from token to representation). This paper is exciting because they were able to create a multi-lingual embedding space that used contextual word embeddings.
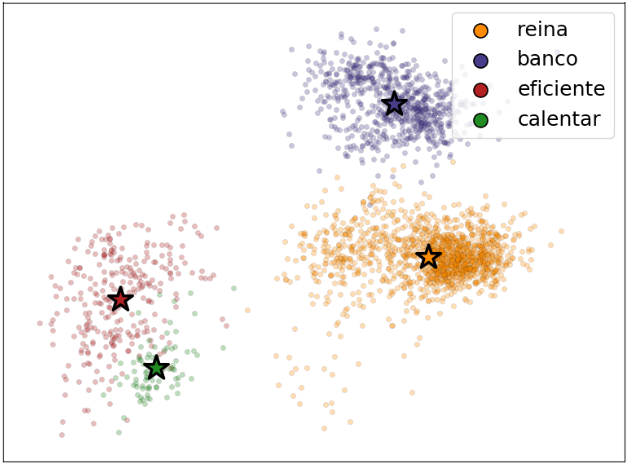
Each token will have a “point cloud” of embedding values, one point for each context containing the token. They define the embedding anchor as the average of all those points for a particular token. Here’s a figure from the paper that displays a two-dimensional PCA of the contextual representations for four Spanish words, along with their anchors:
The authors then list some key properties of this learned contextualized embedding:
- The point clouds are well separated, meaning that contextualized points tend to be much closer to their anchors than anchors are to each other.
- Distinct senses for the same word are separated into distinct clouds, and those clouds are aligned with their corresponding distinct senses or words in the target language.
context-independent alignment
Whether a dictionary is available or not, the authors assume a linear transformation exists between languages; that is, for an embedding \(\mathbf e_i^s\) of token \(i\) in language \(s\), the embedding \(\mathbf e_i^t\) in language \(t\) is approximated by \(W\mathbf e_i^s\), where \(W\) is learned. The learned transition matrix \(W^{s\rightarrow t}\) can be found by solving the following optimization problem:
where \(O_d(\mathbb R)\) is the space of orthogonal matrices. This makes the solution \(W^{s\rightarrow t}=UV^\top\) where \(U\) and \(V\) are the \(U\) and \(V\) from the SVD of the multiplication of the source and (transposed) target embedding matrices. This can be calculated directly if there is a dictionary, but if there is none adversarial training can generate a dictionary to trick a discriminator trained to distinguish between embeddings from the target and embeddings from aligned source.
context-dependent alignment
In the supervised case (with a dictionary), you can just use the anchors discussed above as the \(e_i\) values. And since \(W^{s\rightarrow t}\) is constrained to be orthogonal, relationships between contextual embeddings are preserved across transformations into the target language.
In the unsupervised case they used multiple embeddings induced by different contexts, but the training was less stable than the anchor version.
a shared pretrained embedding
In the previous discussion the authors started from separate pretrained embeddings for each language, but in the case of a low-resource language it could be useful to learn a shared embedding for both languages that allows the low-resource language to benefit from the structure of the higher-resource language.
Our key idea is to constrain the embeddings across languages such that word translations will be close to each other in the embedding space.
They implement this as an actual regularization term for the loss function (with \(\mathbf v_i^s\) being the word representation prior to the context-aware part):
multilingual parsing with alignment
To train a multilingual model to produce these embeddings, they align the contextual word embeddings for all languages in a joint space. The contextual word embeddings are obtained through a language-specific linear transformation to the joint space \(J\):
This alignment is learned by applying the regularization described above, prior to the parser training. For their experiments, they use the space of the training language as the joint space, and align the tested language to it.
results
The unsupervised context-based model performed better on some languages than the anchored one, but failed to converge on Swedish.
In the zero-shot case, the parser was trained on the five other languages plus English, and the embeddings for all six languages were aligned to English. The model outperformed all others in five of the six languages, even without supervised alignment with a dictionary or POS tags. The one language where performance decreased was also the language that had the best LAS scores.
In the extremely low-resource setting of Kazakh, the model improved LAS-F1 from 31.93 to 36.98. This tree-bank only has 38 trees in the training set, and no POS tags.
The model also drastically improves scores over limited unlabeled data, as evidenced by the Spanish results.